Все дедуктивные умозаключения называются силлогизмами (от греч. sillogismos – подсчитывание, подытоживание, выведение следствия). Существует несколько видов силлогизмов. Первый из них называется простым (категорическим), потому что все, входящие в него суждения (две посылки и вывод) являются простыми, или категорическими. Это уже известные нам суждения видов А, I, Е, О.
Рассмотрим пример простого силлогизма:
Все цветы (М) – это растения (Р).
Все розы (S) – это цветы (М).
Все розы (S) – это растения (Р).
Обе посылки и вывод являются в данном силлогизме простыми суждениями (причем и посылки, и вывод – это суждения вида А (общеутвердительные)). Обратим внимание на вывод, представленный суждением: «Все розы – это растения». В этом выводе субъектом выступает термин «розы», а предикатом – термин «растения». Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Также в обеих посылках повторяется термин «цветы», который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщенные в посылках термины «растения» и «розы» можно связать в выводе. Таким образом, структура силлогизма включает в себя две посылки и один вывод, которые состоят из трех (различным образом расположенных) терминов:
- Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма (вторая посылка также называется меньшей).
- Предикат вывода располагается в первой посылке силлогизма и называется большим термином силлогизма (первая посылка также называется большей). Предикат вывода, как правило, является по объему большим понятием, чем субъект вывода (в приведенном примере понятия «розы» и «растения» находятся в отношении родовидового подчинения), в силу чего предикат вывода назван большим термином, а субъект вывода – меньшим.
- Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизма и обозначается латинской буквой М, потому что «средний» на латинском – это medium.
Три термина силлогизма могут быть расположены в нем по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма. Таких фигур четыре, т. е. все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Рассмотрим их.
Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например:
Все газы (М) – это химические элементы (Р).
Гелий (S) – это газ (М).
Гелий (S) – это химический элемент (Р).
Учитывая, что в первой посылке средний термин связан с предикатом, во второй субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведенном примере (рис. 34):
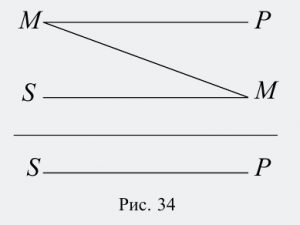
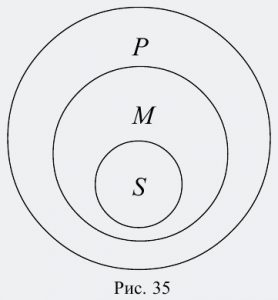
Прямые линии на схеме (за исключением той, которая отделяет посылки от вывода) показывают связь терминов в посылках и в выводе. Поскольку роль среднего термина заключается в том, чтобы связывать больший и меньший термины силлогизма, то на схеме средний термин в первой посылке соединяется линией со средним термином во второй посылке. Схема показывает, каким именно образом средний термин связывает между собой другие термины силлогизма в его первой фигуре. Кроме того, отношения между тремя терминами можно изобразить с помощью кругов Эйлера. В данном случае получится следующая схема (рис. 35):
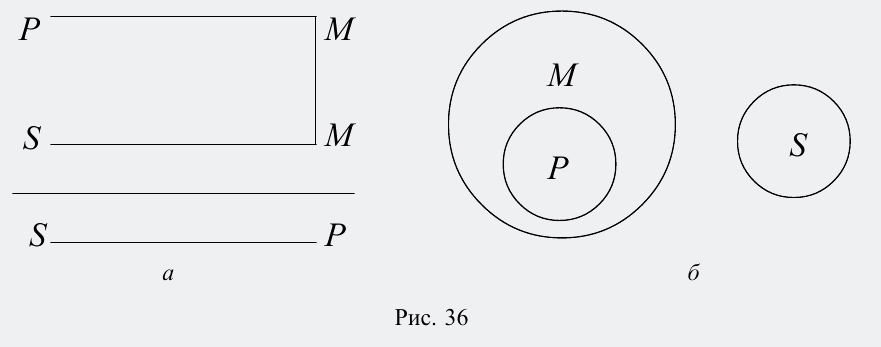
Вторая фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином. Например:
Все рыбы (Р) дышат жабрами (М).
Все киты (S) не дышат жабрами (М).
Все киты (S) не рыбы (Р).
Схемы взаимного расположения терминов и отношений между ними во второй фигуре силлогизма выглядят так (рис. 36):
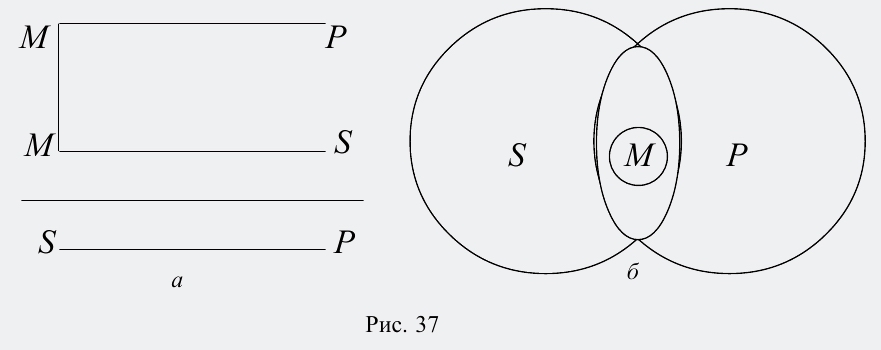
Третья фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например:
Все тигры (М) – это млекопитающие (Р).
Все тигры (М) – это хищники (S).
Некоторые хищники (S) – это млекопитающие (Р).
Схемы взаимного расположения терминов и отношений между ними в третьей фигуре силлогизма (рис. 37):
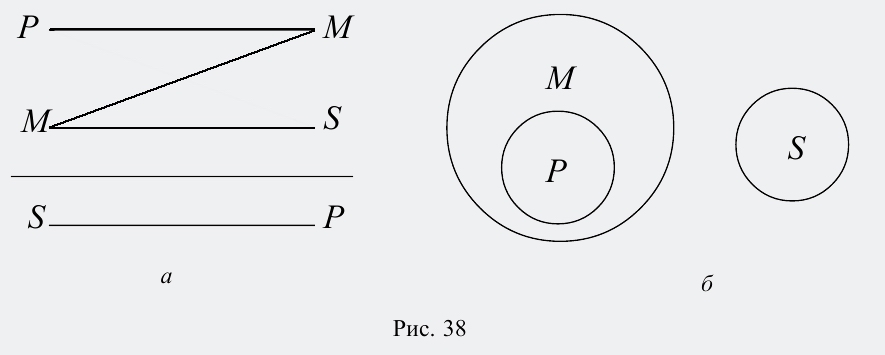
Четвертая фигура силлогизма – это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Например:
Все квадраты (Р) – это прямоугольники (М).
Все прямоугольники (М) – это не треугольники (S).
Все треугольники (S) – это не квадраты (Р).
Схемы взаимного расположения терминов и отношений между ними в четвертой фигуре силлогизма (рис. 38):
Отметим, что отношения между терминами силлогизма во всех фигурах могут быть и другими.
Любой простой силлогизм состоит из трех суждений (двух посылок и вывода). Каждое из них является простым и принадлежит к одному из четырех видов (А, I, Е, О). Набор простых суждений, входящих в силлогизм, называется модусом простого силлогизма.
Например:
Все небесные тела движутся.
Все планеты – это небесные тела.
Все планеты движутся.
В силлогизме первая посылка является простым суждением вида А (общеутвердительным), вторая посылка – это тоже простое суждение вида А, и вывод в данном случае представляет собой простое суждение вида А. Поэтому рассмотренный силлогизм имеет модус ААА.
Во втором примере:
Все журналы – это периодические издания.
Все книги не являются периодическими изданиями.
Все книги не являются журналами.
Силлогизм имеет модус АЕЕ.
В третьем примере:
Все углероды – простые тела.
Все углероды электропроводны.
Некоторые электропроводники – простые тела.
Силлогизм имеет модус ААI.
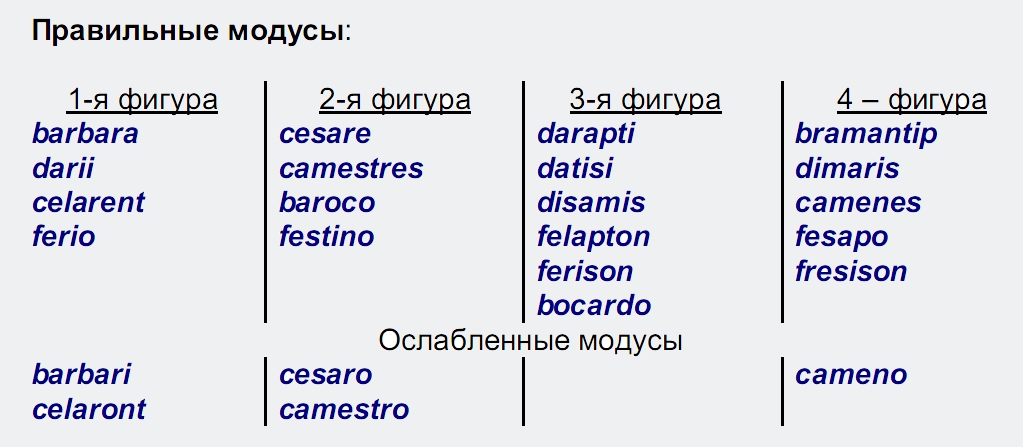
Всего модусов во всех четырех фигурах, т. е. возможных комбинаций простых суждений в силлогизме, – 256. В каждой фигуре 64 модуса. Однако из этих 256 модусов только 19 дают достоверные выводы, остальные приводят к вероятностным выводам. Если принять во внимание, что одним из главных признаков дедукции (а значит, и силлогизма) является достоверность ее выводов, то становится понятным, почему эти 19 модусов называются правильными, а остальные – неправильными.
Иногда выделяют ещё так называемые ослабленные модусы.
Кроме того, модусы иногда называют латинскими словами, гласные буквы которых указывают на тип высказываний в силлогизме (смотри таблицу)
Раньше для запоминания этих модусов гимназистам предлагалось выучить наизусть следующее латинское стихотворение:
Barbara, Celarenr, Darii, Ferio prioris;
Cesare, Camestres, Festino, Baroko sekunda;
Tertia Darapti, Disamis, Datisi, Felapton,
Bokardo, Ferison habet; qvarta insuper addit
Bramantip, Camenes, Dimares, Fesaro, Fresison.
Наша задача – уметь определять фигуру и модус любого простого силлогизма. Например, требуется установить фигуру и модус силлогизма:
Все вещества состоят из атомов.
Все жидкости – это вещества.
Все жидкости состоят из атомов.
Прежде всего, надо найти субъект и предикат вывода, т. е. меньший и больший термины силлогизма. Далее следует установить местоположение меньшего термина во второй посылке и большего – в первой. После этого можно определить средний термин и схематично изобразить расположение всех терминов в силлогизме (рис. 39):
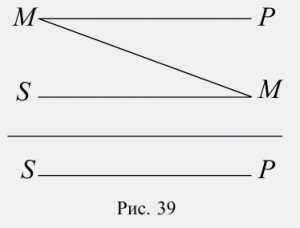
Все вещества (М) состоят из атомов (Р).
Все жидкости (S) – это вещества (М).
Все жидкости (S) состоят из атомов (Р).
Как видим, рассматриваемый силлогизм построен по первой фигуре. Теперь надо найти его модус. Для этого следует выяснить, к какому виду простых суждений относятся первая и вторая посылки и вывод. В нашем примере обе посылки и вывод являются суждениями вида А (общеутвердительными), т. е. модус данного силлогизма – ААА. Итак, предложенный силлогизм имеет первую фигуру и модус ААА.
В латинских названия модусов силлогизма значение имели не только гласные но и согласные буквы. Согласные буквы помогали в сведении фигур силлогизма. Что это такое?
Сведение фигур силлогизма
Дело в том, что наиболее очевидными и понятными выглядят выводы по фигуре I силлогизма. Поэтому когда возникают сомнения в заключениях, которые проведены по другим фигурам, следует свести их к фигуре I. В названиях модусов заключен код, по которому проводится это сведение.
Возьмем силлогизм:

Модус этого силлогизма ААI. Название в соответствии с латинским стихотворением — Darapti.
Ниже приведены правила сведения.
- Первая буква показывает, к какому модусу фигуры I следует свести данный силлогизм. Следовательно, этот силлогизм следует свести к модусу Darii.
- S показывает, что стоящее перед ним суждение должно подвергнуться простому обращению.
- Р показывает, что стоящее перед ним суждение должно подвергнуться обращению через ограничение.
- М показывает, что посылки следует переместить, т. е. большую сделать меньшей, а меньшую большей.
- К показывает, что следует использовать прием сведения к абсурду.
С большей посылкой никаких операций проводить не нужно. Меньшую посылку следует подвергнуть обращению через ограничение, так как оно стоит перед буквой Р. Тогда суждение «Все киты живут в воде» примет вид «Некоторые живущие в воде животные — киты».
С заключением ничего делать не нужно.
Тогда вновь образованный силлогизм примет следующий вид:
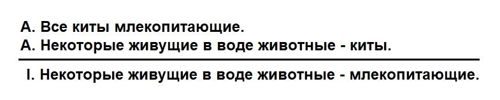
Силлогизм принял вид фигуры I и стал очевидным.



