Любое высказывание или целое рассуждение можно подвергнуть формализации. Это значит отбросить его содержание и оставить только его логическую форму, выразив ее с помощью уже известных нам условных обозначений конъюнкции, нестрогой и строгой дизъюнкции, импликации, эквиваленции и отрицания.
Например, чтобы формализовать следующее высказывание: «Он занимается живописью, или музыкой, или литературой», – надо сначала выделить входящие в него простые суждения и установить вид логической связи между ними. В приведенное высказывание входят три простых суждения: «Он занимается живописью», «Он занимается музыкой», «Он занимается литературой». Эти суждения объединены разделительной связью, однако они друг друга не исключают (можно заниматься и живописью, и музыкой, и литературой), следовательно, перед нами – нестрогая дизъюнкция, форму которой можно представить следующей условной записью: а \/ в \/ с, где а, в, с – указанные выше простые суждения. Форму: а \/ в \/ с, можно наполнить каким угодно содержанием, например: «Цицерон был политиком, или оратором, или писателем», «Он изучает английский, или немецкий, или французский», «Люди передвигаются наземным, или воздушным, или водным транспортом».
Формализуем рассуждение: «Он учится в 9 классе, или в 10 классе, или в 11 классе. Однако, известно, что он не учится ни в 10, ни в 11 классе. Следовательно, он учится в 9 классе». Выделим простые высказывания, входящие в это рассуждение и обозначим их маленькими буквами латинского алфавита: «Он учится в 9 классе (а)», «Он учится в 10 классе (в)», «Он учится в 11 классе (с)». Первая часть рассуждения представляет собой строгую дизъюнкцию этих трех высказываний: а \/ в \/ с. Вторая часть рассуждения является отрицанием второго: ¬в, и третьего: ¬с, высказываний, причем эти два отрицания соединяются, т. е. связаны конъюнктивно: ¬ в /\ ¬ с. Конъюнкция отрицаний присоединяется к упомянутой выше строгой дизъюнкции трех простых суждений: (а \/ в \/ с) /\ (¬ в /\ ¬ с), и уже из этой новой конъюнкции как следствие вытекает утверждение первого простого суждения: «Он учится в 9 классе». Логическое следование, как мы уже знаем, представляет собой импликацию. Таким образом, результат формализации нашего рассуждения выражается формулой: ((а \/ в \/ с) /\ (¬ в /\¬ с)) → а. Эту логическую форму можно наполнить любым содержанием. Например: «Впервые человек полетел в космос в 1957 г., или в 1959 г., или в 1961 г. Однако, известно, что впервые человек полетел в космос не в 1957 г. и не в 1959 г.. Следовательно, впервые человек полетел в космос в 1961 г.» Еще один вариант: «Философский трактат «Критика чистого разума» написал то ли Иммануил Кант, то ли Георг Гегель, то ли Карл Маркс. Однако, ни Гегель, ни Маркс не являются авторами этого трактата. Следовательно, его написал Кант».
Результатом формализации любого рассуждения, как мы увидели, является какая-либо формула, состоящая из маленьких букв латинского алфавита, выражающих входящие в рассуждение простые высказывания, и условных обозначений логических связей между ними (конъюнкции, дизъюнкции и др.). Все формулы делятся в логике на три вида:
- Тождественно-истинные формулы являются истинными при всех наборах истинностных значений входящих в них переменных (простых суждений). Любая тождественно-истинная формула представляет собой логический закон.
- Тождественно-ложные формулы являются ложными при всех наборах истинностных значений входящих в них переменных. Тождественно-ложные формулы представляют собой отрицание тождественно-истинных формул и являются нарушением логических законов.
- Выполнимые (нейтральные) формулы при различных наборах истинностных значений входящих в них переменных являются то истинными, то ложными.
Если в результате формализации какого-либо рассуждения получается тождественно-истинная формула, то такое рассуждение является логически безупречным. Если же результатом формализации будет тождественно-ложная формула, то рассуждение следует признать логически неверным (ошибочным). Выполнимая (нейтральная) формула свидетельствует о логической корректности того рассуждения, формализацией которого она является.
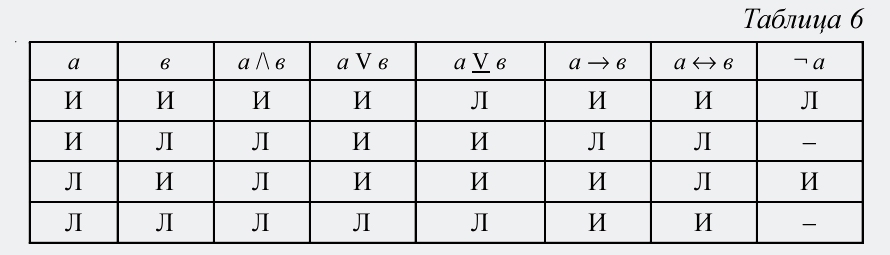
Для того чтобы определить, к какому виду относится та или иная формула, и, соответственно, оценить логическую верность какого-то рассуждения, обычно составляют специальную таблицу истинности для этой формулы. Рассмотрим следующее рассуждение: «Владимир Владимирович Маяковский родился в 1891 г. или в 1893 г. Однако известно, что он родился не в 1891 г. Следовательно, он родился в 1893 г.». Формализуя это рассуждение, выделим входящие в него простые высказывания: «Владимир Владимирович Маяковский родился в 1891 г.». «Владимир Владимирович Маяковский родился в 1893 г.». Первая часть нашего рассуждения, несомненно, представляет собой строгую дизъюнкцию этих двух простых высказываний: а \/ в. Далее к дизъюнкции присоединяется отрицание первого простого высказывания, и получается конъюнкция: (а \/ в) /\ ¬ а. И, наконец, из этой конъюнкции вытекает утверждение второго простого суждения, и получается импликация: ((а \/ в) /\ ¬ а) → в, которая и является результатом формализации данного рассуждения. Теперь надо составить табл. 7 истинности для получившейся формулы:

Количество строк в таблице определяется по правилу: 2n, где n – число переменных (простых высказываний) в формуле. Поскольку в нашей формуле только две переменных, то в таблице должно быть четыре строки. Количество колонок в таблице равно сумме числа переменных и числа логических союзов, входящих в формулу. В рассматриваемой формуле две переменных и четыре логических союза (\/, /\, ¬, →), значит, в таблице должно быть шесть колонок. Первые две колонки представляют собой все возможные наборы истинностных значений переменных (таких наборов всего четыре: обе переменные истинны; первая переменная истинна, а вторая ложна; первая переменная ложна, а вторая истинна; обе переменные ложны). Третья колонка – это истинностные значения строгой дизъюнкции, которые она принимает в зависимости от всех (четырех) наборов истинностных значений переменных. Четвертая колонка – это истинностные значения отрицания первого простого высказывания: ¬ а. Пятая колонка – это истинностные значения конъюнкции, состоящей из вышеуказанной строгой дизъюнкции и отрицания, и, наконец, шестая колонка – это истинностные значения всей формулы, или импликации. Мы разбили всю формулу на составные части, каждая из которых является двучленным сложным суждением, т. е. состоящим из двух элементов (в предыдущем параграфе говорилось о том, что отрицание также представляет собой двучленное сложное суждение):
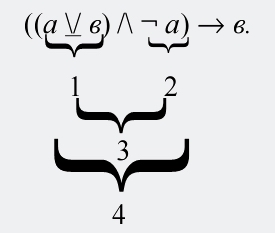

В четырех последних колонках таблицы представлены истинностные значения каждого из этих двучленных сложных суждений, образующих формулу. Сначала заполним третью колонку таблицы. Для этого нам надо вернуться к предыдущему параграфу, где была представлена таблица истинности сложных суждений (см. табл. 6), которая в данном случае будет для нас базисной (как таблица умножения в математике). В этой таблице мы видим, что строгая дизъюнкция ложна, когда обе ее части истинны или обе ложны; когда же одна ее часть истинна, а другая ложна, тогда строгая дизъюнкция истинна. Поэтому значения строгой дизъюнкции в заполняемой таблице (сверху вниз) таковы: «ложно», «истинно», «истинно», «ложно».
Далее заполним четвертую колонку таблицы: ¬ а: когда утверждение два раза истинно и два раза ложно, тогда отрицание ¬ а, наоборот, два раза ложно и два раза истинно. Пятая колонка – это конъюнкция. Зная истинностные значения строгой дизъюнкции и отрицания, мы можем установить истинностные значения конъюнкции, которая истинна только тогда, когда истинны все входящие в нее элементы. Строгая дизъюнкция и отрицание, образующие данную конъюнкцию, одновременно истинны только в одном случае, следовательно конъюнкция один раз принимает значение «истинно», а в остальных случаях – «ложно». Наконец, надо заполнить последнюю колонку: для импликации, которая и будет представлять истинностные значения всей формулы. Возвращаясь к базисной таблице истинности сложных суждений, вспомним, что импликация ложна только в одном случае: когда ее основание истинно, а следствие ложно. Основанием нашей импликации является конъюнкция, представленная в пятой колонке таблицы, а следствием простое суждение (в), представленное во второй колонке. Некоторое неудобство в данном случае заключено в том, что слева направо следствие идет раньше основания, однако мы всегда можем мысленно поменять их местами. В первом случае (первая строчка таблицы, не считая «шапки») основание импликации ложно, а следствие истинно, значит, импликация истинна. Во втором случае и основание, и следствие ложны, значит, импликация истинна. В третьем случае и основание, и следствие истинны, значит, импликация истинна. В четвертом случае, как и во втором, и основание, и следствие ложны, значит, импликация истинна.
Рассматриваемая формула принимает значение «истинно» при всех наборах истинностных значений входящих в нее переменных, следовательно, она является тождественно-истинной, а рассуждение, формализацией которого она выступает, логически безупречно.

Рассмотрим еще один пример. Требуется формализовать следующее рассуждение и установить, к какому виду относится выражающая его формула: «Если какое-либо здание является старым, то оно нуждается в капитальном ремонте. Это здание нуждается в капитальном ремонте. Следовательно, это здание старое». Выделим простые высказывания, входящие в это рассуждение: «Какое-либо здание является старым», «Какое-либо здание нуждается в капитальном ремонте». Первая часть рассуждения представляет собой импликацию: а → в, этих простых высказываний (первое является ее основанием, а второе – следствием). Далее, к импликации присоединяется утверждение второго простого высказывания, и получается конъюнкция: (а → в) /\ в. И наконец, из этой конъюнкции вытекает утверждение первого простого высказывания, и получается новая импликация: ((а → в) /\ в) → а, которая и является результатом формализации рассматриваемого рассуждения. Чтобы определить вид получившейся формулы, составим табл. 8 ее истинности.

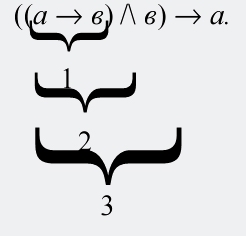
В формуле две переменные, значит, в таблице будет четыре строчки; также в формуле три союза (→, /\, →), значит, в таблице будет пять колонок. Первые две колонки – это истинностные значения переменных. Третья колонка – истинностные значения импликации. Четвертая колонка – истинностные значения конъюнкции. Пятая, последняя колонка – истинностные значения всей формулы – итоговой импликации. Таким образом, мы разбили формулу на три составные части, представляющие собой двучленные сложные суждения: ((а → в) /\ в) → а.
Заполним последовательно три последних колонки таблицы по тому же принципу, что и в предыдущем примере, т. е. опираясь на базисную таблицу истинности сложных суждений (см. табл. 6). Рассматриваемая формула принимает как значение «истинно», так и значение «ложно» при различных наборах истинностных значений входящих в нее переменных, следовательно, она является выполнимой (нейтральной), а рассуждение, формализацией которого она выступает, логически корректно, но небезупречно: при ином содержании рассуждения такая форма его построения могла бы привести к ошибке, например: «Если слово стоит в начале предложения, то оно пишется с большой буквы. Слово «Москва» всегда пишется с большой буквы. Следовательно, слово «Москва» всегда стоит в начале предложения».



